벡터로 두 선분의 교점 구하기

애드혹과 케이스 워크 노가다를 통한 선분 교차 판정은 좀 더럽다. 벡터를 사용해서 케이스를 좀 더 깔끔하게 분류해 선분의 교점을 구해보자.

• 이 글에서는 편의상 원점과 점 $A$를 잇는 벡터 $\overrightarrow{OA}$를 $\overrightarrow{A}$로 표현한다.

요약

원리는 필요 없고 알고리즘만 갖다 쓸 거라면 이걸 그대로 구현하면 된다. 맨 아래에 실제로 작동하는 코드도 있다.

• 입력 - 두 선분 $\overline{P_0 P_1}$과 $\overline{Q_0 Q_1}$
• 출력 - 두 선분의 교점이 있으면 그 교점을, 두 선분이 한 선분으로 겹치면 그 선분을 반환하며, 두 선분이 만나지 않으면 만나지 않는다고 판단한다.

1. $u \leftarrow (\overrightarrow{P_0 P_1} \times \overrightarrow{Q_0 Q_1})$
2. $u \ne 0$이라면,
   1. $s \leftarrow (\overrightarrow{P_0 Q_0} \times \overrightarrow{Q_0 Q_1}) / u \qquad t \leftarrow (\overrightarrow{P_0 Q_0} \times \overrightarrow{P_0 P_1}) / u$
   2. $0 \le s \le 1$이고 $0 \le t \le 1$이면 두 선분은 $\overrightarrow{OP_0} + s\overrightarrow{P_0P_1}$에서 교차한다. 그렇지 않으면 교점이 없다.
3. 그렇지 않다면,
   1. $\overrightarrow{P_0 Q_0} \times \overrightarrow{Q_0 Q_1} = 0$, $\overrightarrow{P_0 Q_0} \times \overrightarrow{P_0 P_1} = 0$ 중 하나라도 거짓이면 교점이 없다.
   2. $A_0, \ A_1 \leftarrow \min(P_0, \ P_1), \ \max(P_0, \ P_1) \ B_0, \ B_1 \leftarrow \min(Q_0, \ Q_1), \ \max(Q_0, \ Q_1)$
   3. $L \leftarrow \max(A_0, \ B_0) \ R \leftarrow \min(A_1, \ B_1)$
   4. $L < R$이면 선분 $LR$에서 겹치고, $L = R$이면 $L$이 교점이고, $L > R$이면 교점이 없다. 이 대소비교는 좌표를 튜플로 두고 통째로 비교하는 것이다.

배경 지식

혹시 벡터에 대해 잘 모르는 상황이라면 이 글을 읽고 오는 것을 추천한다. 고등학교 기하 수준의 배경 지식이 있다면 굳이 안 봐도 되긴 하는데, 선분 교차 판정뿐만 아니라 계산 기하 분야에서 자주 등장하는 알고리즘을 종합적으로 설명하고 있어서 한 번 보면 좋다.

두 벡터를 곱하는 방법 중 하나로 외적(cross product)가 있다. 두 평면벡터의 외적은 그냥 수 하나가 나오고, 다음과 같이 정의된다.

\[(a_x, a_y) \times (b_x, b_y) = a_x b_y - a_y b_x\]

외적의 성질은 다음과 같다.

• 벡터의 덧셈에 대해 결합법칙과 분배법칙을 만족한다.
• 외적하는 두 벡터를 교환하면 부호가 반대가 된다. $(\vec{a} \times \vec{b} = - \vec{b} \times \vec{a})$
• 평행한 두 벡터를 외적하면 $0$이 된다.
  • 두 벡터의 외적이 $0$이 아니면 두 벡터는 평행하지 않다.
  • 같은 벡터를 외적하면 $0$이 된다. $(\vec{a} \times \vec{a} = 0)$.

한편, 두 점 $A$와 $B$를 양 끝점으로 하는 선분 위의 임의의 점 $X$는 다음과 같이 표현할 수 있다.

\[\overrightarrow{X} = \overrightarrow{A} + s\overrightarrow{AB} \quad (0 \le s \le 1)\]

풀어서 설명하면, 원점에서 점 $X$까지 가려면 일단 점 $A$까지 간 다음, 선분 $\overline{AB}$을 따라 이동하면 된다는 것이다. 선분은 점의 집합이기 때문에, 다르게 말하면 저 식이 선분 자체를 벡터로 표현한 것이라고 볼 수도 있다.

알고리즘 구성

위 그림과 같이 두 선분 $\overline{P_0 P_1}$과 $\overline{Q_0 Q_1}$이 주어졌을 때 그 교점 $R$이 존재하는지, 존재한다면 어떤 점인지 구할 방법을 생각해보자. 이는 벡터 $\overrightarrow{R}$이 만족하는 방정식을 써서, 그 식을 만족하는 변수가 존재하는지 확인하고 존재한다면 그 값을 구하는 것으로 수행할 수 있다.

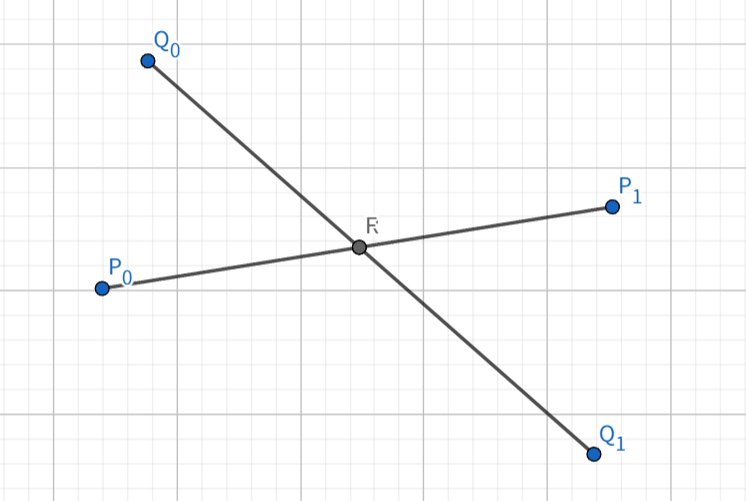
교점 $R$이 존재한다면 다음 두 식을 동시에 만족시키는 실수 $s$와 $t$가 존재한다.

\[\begin{aligned} \overrightarrow{P_0 R} &= s \overrightarrow{P_0 P_1} &\quad (0 \le s \le 1) \\ \overrightarrow{P_0 R} &= \overrightarrow{P_0 Q_0} + t \overrightarrow{Q_0 Q_1} &\quad (0 \le t \le 1) \\ \end{aligned}\]

식을 정리하면 다음과 같다.

\[s \overrightarrow{P_0 P_1} = \overrightarrow{P_0 Q_0} + t \overrightarrow{Q_0 Q_1} \quad (0 \le s, \; t \le 1)\]

여기서 외적의 결합법칙과 같은 벡터를 외적하면 0이 된다는 사실을 이용하면 $s$와 $t$ 중 하나의 변수를 없앨 수 있다. 양변에 $\overrightarrow{Q_0 Q_1}$을 외적하면 $t$가 없어지고 다음 식이 나온다.

\[s (\overrightarrow{P_0 P_1} \times \overrightarrow{Q_0 Q_1}) = (\overrightarrow{P_0 Q_0} \times \overrightarrow{Q_0 Q_1})\]

$\overrightarrow{Q_0 Q_1}$ 대신 $\overrightarrow{P_0 P_1}$을 외적하면 $t$만에 대한 식도 얻을 수 있다.

\[0 = (\overrightarrow{P_0 Q_0} \times \overrightarrow{P_0 P_1}) + t (\overrightarrow{Q_0 Q_1} \times \overrightarrow{P_0 P_1})\] \[-t (\overrightarrow{Q_0 Q_1} \times \overrightarrow{P_0 P_1}) = t (\overrightarrow{P_0 P_1} \times \overrightarrow{Q_0 Q_1}) = (\overrightarrow{P_0 Q_0} \times \overrightarrow{P_0 P_1})\]

만약 $\overrightarrow{P_0 P_1} \times \overrightarrow{Q_0 Q_1} \neq 0$이라면 $s$와 $t$를 바로 구할 수 있다. 여기서부터 $\overrightarrow{P_0 P_1} \times \overrightarrow{Q_0 Q_1} \neq 0$인 경우, $\overrightarrow{P_0 P_1} \times \overrightarrow{Q_0 Q_1} = 0$인 경우로 케이스를 나눠서 풀어보자.

$\overrightarrow{P_0 P_1} \times \overrightarrow{Q_0 Q_1} \neq 0$인 경우

$\overrightarrow{P_0 P_1} \times \overrightarrow{Q_0 Q_1} \neq 0$인 경우는 두 선분 $\overline{P_0 P_1}$과 $\overline{Q_0 Q_1}$이 둘 다 길이가 $0$이 아니고 평행하지 않은 경우다. 이 경우엔 앞서 나온 식으로 $s$와 $t$를 바로 계산할 수 있습니다.

\[s = \frac{ \overrightarrow{P_0 Q_0} \times \overrightarrow{Q_0 Q_1} } { \overrightarrow{P_0 P_1} \times \overrightarrow{Q_0 Q_1} } \qquad t = \frac{ \overrightarrow{P_0 Q_0} \times \overrightarrow{P_0 P_1} } { \overrightarrow{P_0 P_1} \times \overrightarrow{Q_0 Q_1} }\]

$0 \leq s, \; t \leq 1$이면 교점이 존재하는 것이고, 그렇지 않으면 교점이 없다. 교점의 좌표 $R$은 $\overrightarrow{R} = \overrightarrow{P_0} + s\overrightarrow{P_0 P_1}$로 구할 수 있다.

그 외의 경우

$\overrightarrow{P_0 P_1} \times \overrightarrow{Q_0 Q_1} = 0$인 경우는 두 선분이 평행하거나 길이가 $0$인 경우다. 이 경우엔 두 선분이 겹치는지, 겹치지 않는지를 판단해야 한다.

일단, 네 점이 모두 한 직선 위에 있는지 판단해야 한다. 이는 네 점 $P_0$, $P_1$, $Q_0$, $Q_1$중 세 점을 고르는 모든 경우에 대해 외적이 $0$인지 보면 된다. 즉,

\[\begin{aligned} \overrightarrow{P_0 P_1} \times \overrightarrow{P_1 Q_0} &= 0 \\ \overrightarrow{P_0 P_1} \times \overrightarrow{P_1 Q_1} &= 0 \\ \overrightarrow{Q_0 Q_1} \times \overrightarrow{Q_1 P_0} &= 0 \\ \overrightarrow{Q_0 Q_1} \times \overrightarrow{Q_1 P_1} &= 0 \\ \end{aligned}\]

이 네 등식이 모두 성립하는 지 보면 된다.

위 네 식 중 하나라도 성립하지 않으면 네 점이 한 직선 위에 있지 않은 것인데, 두 선분이 평행하지 않은 경우는 앞에서 이미 걸렀으므로 이때는 반드시 두 선분이 평행하고 만나지 않는 경우다. 따라서 이 때는 교점이 존재하지 않는다.

마지막으로 네 점이 한 직선 위에 있는 경우만 남았다.

$A_0 = \min(P_0, P_1)$, $A_1 = \max(P_0, P_1)$, $B_0 = \min(Q_0, Q_1)$, $B_1 = \max(Q_0, Q_1)$로 두자.. 이때 점의 비교 기준은 우선 $x$좌표가 작은 것이 더 작은 점이고, $x$좌표가 같다면 $y$좌표가 작은 것이 더 작은 점이다. 이렇게 하면 $\overrightarrow{A_0 A_1}$과 $\overrightarrow{B_0 B_1}$의 방향이 같아진다.

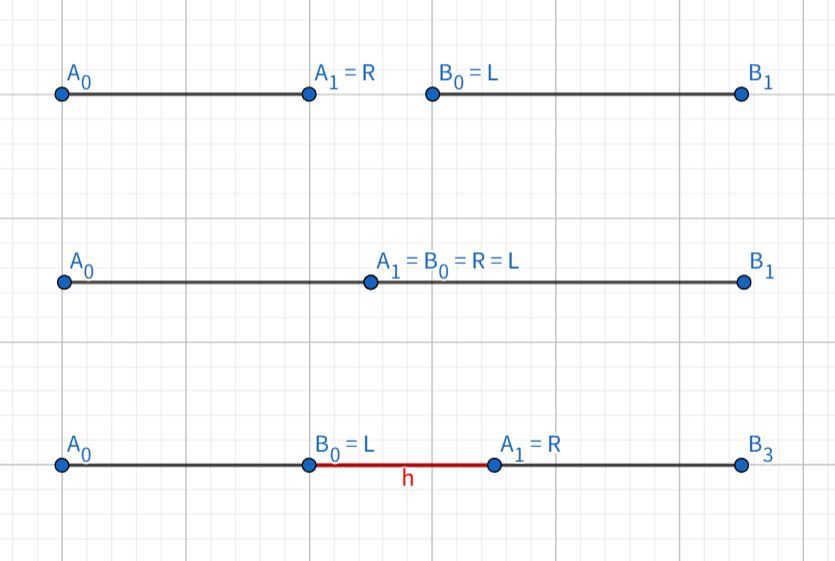
그런 다음, $L = \max(A_0, B_0)$, $R = \min(A_1, B_1)$이라고 하자. $L \leq R$이면 두 선분이 겹치는 것이고, $L = R$이면 교점이 $L$이고, $L > R$이면 교점이 없다.

오버플로 주의

내부 계산을 정수형 또는 분수로만 진행한다면 오버플로가 좀 많이 날 수 있다. 점의 좌표 범위가 $10^9$ 이내라면, $s$와 $t$의 분자는 최대 $10^{18}$, 교점의 좌표는 여기에 벡터를 다시 곱하므로 분자가 최대 $10^{27}$까지 늘어난다. 최종 답안이 정확한 분수 형태일 필요가 없다면 적당한 타이밍에 부동소수점으로 바꿔주자. 최종 답안도 분수 형태로 만들고 싶다면 입력값으로 주어지는 좌표의 세제곱까지 처리할 수 있어야 한다. 예를 들어, 입력값의 범위가 i32라면 마지막에는 i128로 계산해야 한다.

이런 게 귀찮으면 파이썬 등 BigInt를 지원하는 언어를 쓰자.

구현

using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<ll, ll> pll;
typedef pair<ld, ld> pld; 

ll cross(pll a, pll b) {
    return a.first * b.second - a.second * b.first;
}

pll sub(pll a, pll b) {
    return {a.first - b.first, a.second - b.second};
}

// {0, {0, 0}}: no intersection
// {1, {x, y}}: intersection at (x, y)
// {2, {0, 0}}: two segments are overlapped (infinite intersections)
pair<int, pld> intersect(pll p0, pll p1, pll q0, pll q1) {
    pll u = sub(p1, p0);
    pll v = sub(q1, q0);
    ll det = cross(u, v);
    if (det < 0) {
        p0.swap(p1);
        u.first *= -1;
        u.second *= -1;
        det *= -1;
    }
    if (det != 0) {
        pll w = sub(q0, p0);
        ll cross_wu = cross(w, u);
        ll cross_wv = cross(w, v);
        if (cross_wu < 0 || cross_wu > det || cross_wv < 0 || cross_wv > det) {
            return {0, {0, 0}};
        }
        ld s = (ld)cross_wv / det;
        ld t = (ld)cross_wu / det;
        return {1, {p0.first + u.first * s, p0.second + u.second * s}};
    } else {
        if (cross(sub(q0, p0), u) != 0 || cross(sub(q0, p1), u) != 0 || cross(sub(p0, q0), v) != 0 || cross(sub(p0, q1), v) != 0) {
            return {0, {0, 0}};
        }
        pll a0 = min(p0, p1);
        pll a1 = max(p0, p1);
        pll b0 = min(q0, q1);
        pll b1 = max(q0, q1);
        pll l = max(a0, b0);
        pll r = min(a1, b1);
        if (l < r) {
            return {2, {0, 0}};
        } else if (l == r) {
            return {1, {(ld)l.first, (ld)l.second}};
        }
        return {0, {0, 0}};
    }
}